Matéria 3º Matemática

Geometria Analítica

Plano Cartesiano

 
René Descartes

Criado por René Descartes, o plano cartesiano consiste em dois eixos perpendiculares, sendo o horizontal chamado de eixo das abscissas e o vertical de eixo das ordenadas.

O plano cartesiano foi desenvolvido por Descartes no intuito de localizar pontos num determinado espaço. As disposições dos eixos no plano formam quatro quadrantes, mostrados na figura a seguir:

O encontro dos eixos é chamado de origem. Cada ponto do plano cartesiano é formado por um par ordenado (x , y ), onde x: abscissa e y: ordenada.

Marcando pontos no plano cartesiano

Dados os pontos A(3,6), B(2,3), C(-1,2), D(-5,-3), E(2,-4), F(3,0), G(0,5), represente-os no plano cartesiano.

Marcando o ponto A(3,6)
Primeiro: localiza-se o ponto 3 no eixo das abscissas
Segundo: localiza-se o ponto 6 no eixo das ordenadas
Terceiro: Traçar a reta perpendicular aos eixos, o encontro delas será o local do ponto.

O sistema de coordenadas cartesianas possui inúmeras aplicações, desde a construção de um simples gráfico até os trabalhos relacionados à cartografia, localizações geográficas, pontos estratégicos de bases militares, localizações no espaço aéreo, terrestre e marítimo.

Exercícios

1-                Dê as coordenadas de cada ponto no plano cartesiano:

2-                Represente, no plano cartesiano, os pontos:

A (3,4);       B (4,3);       C (-4,1);      D (-2,5);     E (-3,-4);

F (-2,-1);     G (3,-2);     I (0,-5);       J (1,0);                 L (5,-1).

3-                No Exercício anterior:

a)                 Quais pontos pertencem ao 1º quadrante?

A e B

b)                Quais pontos pertencem ao 2º quadrante?

C e D

c)                 Quais pontos pertencem ao 3º quadrante?

E e F

d)                Quais pontos pertencem ao 4º quadrante?

G e L

Igualdade de Pares Ordenados

         Dois pares ordenados são iguais somente se tiverem os primeiros elementos iguais entre si e também os segundos elementos iguais entre si.

Assim:

(a, b) = (c, d) ↔ a=c e b=d

         Exemplo:

Determinar x e y de modo que os pares ordenados ( 2x + 7 , 5y -9 ) e ( x + 3 , 3y -3 ) sejam iguais.

( 2x + 7 , 5y -9 ) = ( x + 3 , 3y -3 )

Então:

2x + 7 = x + 3                        e                 5y -9 = 3y -3

2x - x = + 3 – 7                                      5y -3y  =  -3 + 9

     1x = - 4                                                 2y  =  +6    

       x = - 4                                                  y  =  6/2

                                                                    y  =  + 3

         Logo: x = - 4  e  y = 3 

Exercício

1-                Determine x e y para que cada uma das igualdades seja verdadeira:

a)                 ( x , y ) = ( 8, -6 )

b)                ( 6 , y ) = ( x, 0 )

c)                 ( x , -4 ) = ( - 3, y )

d)                ( 2x , -5 ) = ( 8, y )

e)                 ( x , y +2 ) = ( 5, 9 )

f)                  (3x , 2y) = ( - 12, - 6 )

g)                 ( x – y, 5 ) = ( 0, y )

h)                ( x +1, y -1 ) = ( 3,7 )

i)                   ( x -2, 7 - y ) = ( - 2, 6 )

j)                   ( 3x + 2, 2y – 6 ) = ( 2x  -1, y + 2 )

Correção dos exercícios

a)                 ( x , y ) = ( 8, -6 )

x = 8      e        y = -6

b)                ( 6 , y ) = ( x, 0 )

x = 6                        y = 0

c)                 ( x , -4 ) = ( - 3, y )

x = - 3             y = -4

d)                ( 2x , -5 ) = ( 8, y )

2x = 8                           y = - 5

X =8/2

X = 4

e)                 ( x , y +2 ) = ( 5, 9 )

X = 5            y + 2 = 9

                                          y = 9 – 2

                                          y = 7

f)                  (3x , 2y) = ( - 12, - 6 )

3x = -12                                      2y = -6

X =  -12/3                                       y = -6/2

X = - 4                                        y = -3

g)                 ( x – y, 5 ) = ( 0, y )

X – y = 0      y = 5

X – 5 = 0

X = 5

h)                ( x +1, y -1 ) = ( 3, 7 )

X + 1 = 3                      y -1 = 7

X = 3 -1                        y = 7 +1

X = 2                             y = 8

i)                   ( x -2, 7 - y ) = ( - 2, 6 )

X – 2 = -2                7 - y = 6

X = -2 + 2                - y = 6 -7

X = 0                        - y = - 1

                                 ( -1) – y = -1

                                                   Y = 1

j)                   ( 3x + 2, 2y – 6 ) = ( 2x  -1, y + 2 )

3x + 2 = 2x -1                                  2y – 6 = y + 2

3x – 2x = - 1 – 2                              2y – y = + 2 + 6

         x = - 3                                           y = + 8

Produto Cartesiano

         Sejam A e B dois conjuntos não vazios. Chama-se produto cartesiano de A e B ao conjunto de todos os pares ordenados onde o primeiro elemento pertence a A e o segundo pertence a B.

Indicamos A x B e lemos “A cartesiano de B”.

Exemplo: Sendo A= {1,2} e B= {3,4,5}, temos:

A x B= {(1,3), (1,4), (1,5), (2,3), (2,4), (2,5) }

B x A= {(3,1),(3,2), (4,1), (4,2),(5,1), (5,2 ) }

Distância entre Dois Pontos

Dados dois pontos A( x_a, y_a ) e B( x_b, y_b), vamos determinar a distância d_AB entre eles              __
1º Caso AB é paralelo ao eixo x.

d_AB = [ x_B – x_A ]

2º Caso AB é paralelo ao eixo y.

d_AB = [ y_B – y_A ]

3º Caso AB não paralelo aos eixos. Aplicando o teorema de Pitágoras no triângulo ABC, temos:

d²_AB= d²_AC + d²_BC

Sendo d_AB = [ x_B – x_A ] e d_AB = [ y_B – y_A ] , então

                                             d²_AB = ( x_B – x_A )² + ( y_B – y_A )²

^Exemplos:

^{1-                   Represente os pontos A(7, - 6) e B(2, 6) e calcule a distância  entre eles.}

2-                Represente no plano cartesiano os pontos A(2,5) ,B( 4,-3) e C(-2,-6), vértices do triângulo ABC, e calcule o perímetro desse triângulo.

Lembrando que o perímetro é a soma das medidas dos lados, vamos calcular:

P = 10 +3  +11↔ P = 21 + 3

3-                A distância entre dois pontos A(3,1) e B(x,4) é .

Determine o valor de x (abscissa do ponto B).

X₁=4 e        x₂=2↔  B(2,4)  ou   B(4,4)

Exercícios

1-                Calcule a distância entre os seguintes pontos:

a)                 A(2,3) e B(2,5)

b)                A(2,1) e B(-2,4)

c)                 A(0,6) e B(1,5)

d)                A(6,3) e B(2,7)

e)                 A(4,3) e B(0,0)

f)                  A(-1,-1) e B(1,1)

2-                Calcule o perímetro do triângulo de vértices A(3,2) , B(2,4) , C(3,3).

3-                A distância entre os pontos A(-1,5) , B(0,y) é  determine a ordenada do ponto B.

Exercícios

1-                Calcule a distância entre os seguintes pontos:

a)                 A(2,3) e B(2,5)

b)                A(2,1) e B(-2,4)

c)                 A(0,6) e B(1,5)

d)                A(6,3) e B(2,7)

e)                 A(4,3) e B(0,0)

f)                  A(-1,-1) e B(1,1)

2-                Calcule o perímetro do triângulo de vértices A(3,2) , B(2,4) , C(3,3).

3-                A distância entre os pontos A(-1,5) , B(0,y) é  determine a ordenada do ponto B.

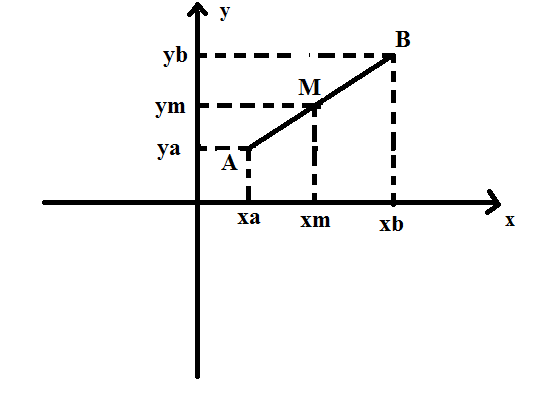
Ponto que Divide um Segmento em Uma Razão Dada

Considere o seguinte problema:

“Dados dois pontos A(x_a , y_a) e B(x_b , y_b), determine as coordenadas x_M e y_M de um ponto M ≠ B, que

                             __

divide o segmento AB na razão dada r = ”.

Na figura abaixo, sendo ΔMPB temos:

Coordenadas de M:

Caso particular: Ponto Médio          ___

Se M é o ponto médio do segmento AB, então a r = 1, uma vez que AM = MB        e       r = .

Substituindo r = 1 nas expressões I e II, coordenadas de M, temos as coordenadas do ponto médio do segmento AB:

Exemplos:

1-                Dados os pontos A(3,-4) e B(-2,-7), determine M(x_M ,y_M) que divide o segmento AB na razão r=5.

Dos dados do problema, Temos:

x_a = 3 ; y_a = -4 ; x_b = -2 ; y_b = -7 e r = 5

2-                Determine o ponto médio do segmento PR, sendo P(3,6) e R(2,-8).

Dos dados do problema, Temos:

x_a = 3 ; y_a = 6 ; x_b = 2 ; y_b = -8 e r = 1

3-                Sendo M(2,4) o ponto médio de AB, onde A(1,-6), determine as coordenadas de B.

         

                                                     Exercícios

1-                Determine as coordenadas de um ponto M que divide um segmento AB na razão r, nos seguintes casos:

a)                 A(3,5),   B(6,5)         e r = 2

b)                A(4,1),   B(7,0)         e r = 4

c)                 A(-3,-2),          B(-4,5)        e r = -3

d)                A(4,-1), B(-3,6)        e r = -2